Análisis sintáctico de un compilador

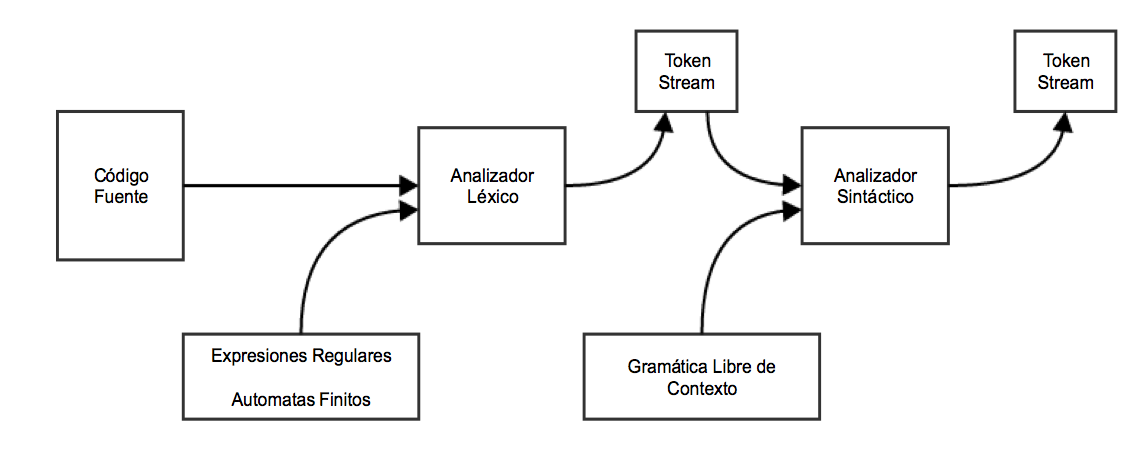
El análisis sintáctico o “parseo” es la segunda fase de un compilador. En este post aprenderemos los conceptos básicos que se usan en la construcción de un parser.

Hemos visto que un analizador léxico puede identificar tokens con la ayuda de expresiones regulares y reglas de patrones. Pero un analizador léxico no puede revisar la sintaxis para una sentencia dadas las limitaciones que las expresiones regulares presentan. Las expresiones regulares no pueden revisar el balanceo de tokens, como paréntesis llaves y corchetes, entonces esta fase utiliza una gramática libre de contexto la cual es reconocida por un automata “push-down”

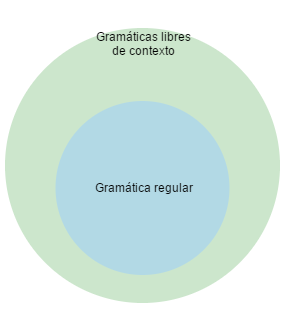
Las gramáticas libres de contexto por otra parte, pueden ser un super-conjunto de una gramatica regular:

Esto implica que para cada gramática regular existe una gramática libre de contexto, pero existen problemas que están mas allá del alcance de una gramática regular.  Las gramáticas libres de contextos constituyen una herramienta útil para describir la sintaxis de los lenguajes de programación.

Gramáticas libres de contexto

Una gramática libre de contexto tiene cuatro elementos básicos:

• Un conjunto de no terminales(V). Los no terminales son variables sintácticas que denotan conjuntos de cadenas de texto que ayudan a definir el lenguaje generado por la gramática.
• Un conjunto de tokens, conocidos como símbolos terminales (?). Los símbolos terminales son los símbolos básicos con los cuales las cadenas de texto son formadas.
• Un conjunto de producciones (P).  Las producciones de una gramática especifican la forma en la cual los no terminales pueden ser combinados para formar cadenas. Cada producción consiste de no terminales, a los que llamamos lado izquierdo de la producción, luego una flecha, seguida de una secuencia de tokens y/o terminales a los que llamamos lado derecho de la producción.
• Uno de los no terminales es designado como el símbolo de inicio (S) desde el cual comienza la producción.

Las cadenas son derivadas del símbolo de inicio repitiendo y reemplazando no terminales en el lado derecho de la producción por otro no terminal o un terminal.

Ejemplo: Tomemos el problema del lenguaje de palíndromos, el cual no puede ser descrito por una expresión regular. Esto es:  L = { w | w = w^R } no es un lenguaje regular, pero puede ser descrito por una gramática libre de contexto como lo ilustramos a continuación:

G = ( V, ?, P, S )

Donde:

V = { Q, Z, N }
? = { 0, 1 }
P = { Q -> Z | Q -> N | Q -> ? | Z -> 0Q0 | N -> 1Q1 }
S = { Q }

Donde ? representa una cadena vacía o un espacio (se numeraron las reglas de producción para su posterior análisis).

Esta gramática describe el lenguaje de palíndromos, tales como: 1001, 11100111, 00100, 1010101, 11111, etc.

Si tomamos por ejemplo el palindromo de 0s y 1s: 1001

tomamos como producción inicial la regla 2 “Q produce N”, luego la regla 5 “N produce 1Q1” y en esta reemplazamos Q por la regla 1 “Q produce Z” y luego nos vamos a la regla 4 para reemplazar la Z y vemos que “Z produce 0Q0”, finalmente reemplazamos esa ultima Q por la regla 3 “Q produce vacío” y el palíndromo 1001 pasaría su análisis sintáctico como un palíndromo valido.

Analizadores sintácticos

Un analizador sintáctico o “parser” toma como entrada la salida de un analizador léxico en la forma de streams de tokens.  El parser compara el código fuente (stream de tokens) contra las reglas de producción de la gramática para detectar cualquier error en el código.  La salida de un analizador sintáctico es entonces un “árbol de parseo”.

De esta forma el parser logra realizar varias tareas: parsea el código, detecta errores y generar un árbol de parseo que seria la salida de esta fase del compilador.

Se espera que los parsers procesen todo el código aun si existen algunos errores en el programa utilizando estrategias para la recuperación de errores, de las cuales hablaremos mas adelante.

Derivación

Una derivación es básicamente una secuencia de reglas de producción, útiles para obtener la cadena de entrada. Durante el praseo, se toman dos desiciones esenciales para alguna forma de entrada:

• Cual será el no terminal que reemplazaremos
• Cual será la regla de producción que reemplazara a un no terminal

Derivación más a la izquierda

Si la forma sentencial de una entrada es escaneada y reemplazada de izquierda a derecha se le llama “derivación mas a la izquierda”. La forma sentencial derivada por la derivación de la izquierda se llama forma de sentencia izquierda.

Derivación más a la derecha

Si analizamos y reemplazamos la entrada con reglas de producción, de derecha a izquierda, se conoce como derivación “más a la derecha”. La forma sentencial derivada de la derivación más a la derecha se llama la forma sentencial derecha.

Ejemplo

Reglas de producción:

E -> E + E
E -> E * E
E -> id

Cadena de entrada: “1 + 2 * 3”

La derivación más a la izquierda es:

E -> E * E
E -> E + E * E
E -> id + E * E
E -> id + id * E
E -> id + id * id

Hay que notar que el no terminal mas a la izquierda siempre es procesado de primero.

La derivación mas a la derecha sería:

E -> E + E
E -> E + E * E
E -> E + E * id
E -> E + id * id
E -> id + id * id

Árbol De Parseo

Un árbol de parseo es la representación gráfica de una derivación. Es conveniente ver como las cadenas son derivadas a partir del símbolo de inicio. El símbolo de inicio de la derivación se convierte en la raíz del árbol de parseo.

Ejemplo:

Tomaremos la derivación mas a la izquierda de:  a + b * c

E -> E * E
E -> E + E * E
E -> id + E * E
E -> id + id * E
E -> id + id * id

paso 1 

E ->  E * E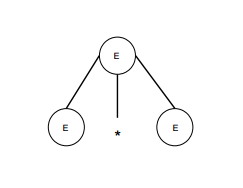

paso 2

E -> E + E * E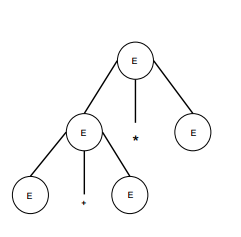

paso 3

E -> id + E * E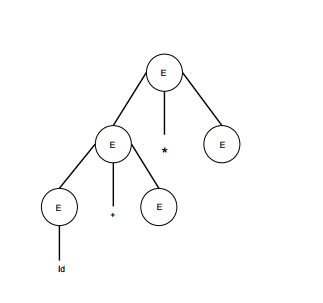

paso 4

E -> id + id * E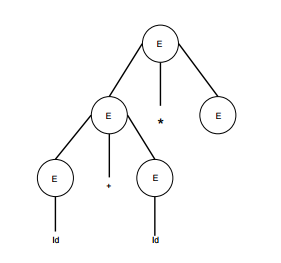

paso 5

E -> id + id * id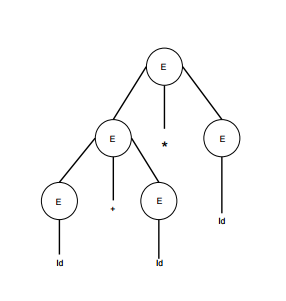

En un árbol de parseo:

• Todas las hojas son símbolos terminales
• Todos los nodos interiores son no terminales
• El recorrido in-order  da como resultado la cadena de entrada original

Estos arboles manejan la asociatividad y la precedencia de operadores. El sub-árbol mas profundo es recorrido de primero, por lo cual los operadores de ese árbol obtienen precedencia sobre los operadores de sus árboles padre.

Ambigüedad

Una gramática G  es ambigua cuando  tiene mas de un arbol de parseo (ya sea por la izquierda o por la derecha) para al menos una cadena de entrada.

Ejemplo

E -> E + E
E -> E – E
E -> id

Para la cadena id + id – id, la gramática anterior tiene dos árboles de parseo diferentes.

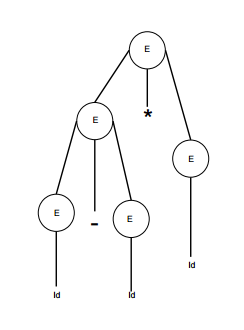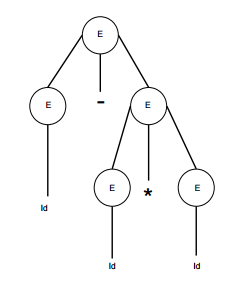El lenguaje generado por una gramática ambigua se llama Inherentemente Ambigua. La Ambiguedad en una gramatica no es buena para la construcción de un compilador. Ningún método puede detectar y remover la ambigüedad automáticamente, pero puede ser removida re-escribiendo toda la gramatica sin ambiguedades, o estableciendo y siguiendo las siguientes restricciones de precedencia y asociatividad.

Asociatividad

Si un operando tiene operadores en ambos lados, el lado en el cual el operador toma su operador se decide por la asociatividad de esos operadores. Si la operación es asociativa por la izquierda, entonces el operando será tomado por la izquierda. Si la operación es asociativa por la derecha tomamos el operador de la derecha.

Ejemplo

Operaciones como la suma, multiplicación, resta y división son asociativas por la izquierda. Si la expresion contiene:

id op id op id

Será evaluada como:

(id op id) op id

Por ejemplo (id + id) + id

Operaciones como los exponenciales son asociativos por la derecha.

ejemplo:

El orden de la evaluación en la misma expresión será:

id op (id op id)

Por ejemplo, id ^ (id ^ id)

Precedencia

Si dos operadores diferentes comparten un mismo operando, la precedencia de los operadores decide cual tomará el operando. Esto es, 2+3*4 puede tener 2 árboles de parseo, uno que corresponde a (2+3)*4 y otro que corresponda a 2+(3*4). Estableciendo la precedencia entre operadores, este problema puede ser resuelto con facilidad. Como en este ejemplo, matemáticamente la multiplicación tiene precedencia sobre la suma, entonces la expresión 2+3*4 siempre sera interpretada de la misma manera.

Esto reduce la posibilidad de tener una gramatica ambigua.

Recursividad por la izquierda

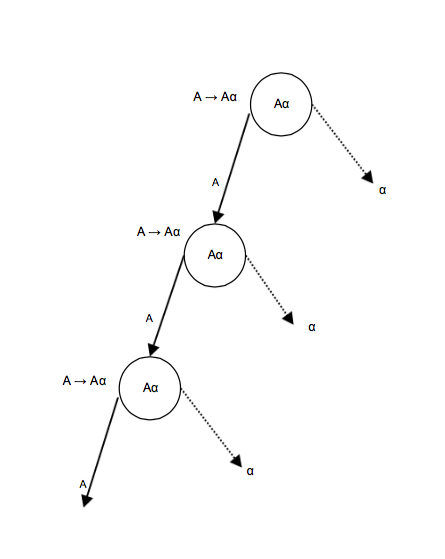
Una gramática se convierte en recursiva por la izquierda si no tiene ningún no-terminal ‘A que contenga una derivación ‘A’ recursiva como el símbolo mas a la izquierda.  Una gramatica recursiva por la izquierda es considerada problemática por los parsers de tipo ‘top down’, estos parsers comienzan parseando desde el símbolo de inicio el cual es un no-terminal. Entonces cuando el parser encuentra el mismo no terminal como producto de una derivación se vuelve complicado juzgar cuándo detener la recursión de parseo del no-terminal a la izquierda, y consecuentemente se convierte en un ciclo infinito.

Consideremos el siguiente ejemplo:

[1] A -> Aa | b
[2] S -> Aa | b 
    A -> Sd

[1] Es un ejemplo de recursión por la izquierda inmediata, donde ‘A’ es cualquier símbolo no-terminal y ‘a’ no representa una cadena para un no-terminal.

[2] Es un ejemplo de recursión por la izquierda indirecta.

Un parser top-down  tomara primero ‘A’ , el cual regresara una cadena que consiste en ‘A’ de nuevo y de esa forma el parser entraría en un ciclo infinito.

Quitando la recursividad por la izquierda

Una forma de quitar la recursividad por la izquierda es utilizar la siguiente técnica:

Dada la produccion:

A -> Aa |
     b

Se convierte en las siguientes producciones

A  -> bA'
A' -> aA' | 
      e

Esto no impacta las cadenas derivadas de la gramatica, pero quita la recursividad por la izquierda.

El segundo método es usar el siguiente algoritmo, el cual debería eliminar todas las recursiones por la izquierda directas e indirectas.

INICIO

Ordenar los no-terminales like A1, A2, A3,…, A<sub>n</sub>

   for each i from 1 to n
      {
      for each j from 1 to i-1
         {
         reemplazar cada producción de la forma: Ai => Ajy
         con Ai ? d1y  | d2y | d3y |…| y 
         donde  Aj ? d1 | d2|…| dn  son las producciones actuales de  Aj  
         }
      }
   eliminar cualquier recursividad por la izquierda inmediata
   
FIN

ejemplo

En las siguientes producciones:

S -> Aa | b
A -> Sd

Después de aplicar el algoritmo descrito

S -> Aa | b 
A -> Aad | bd

Y después quitando toda recursividad por la izquierda aplicando la primera técnica

A -> bdA'
A' -> adA' | e

Ahora las reglas de producción no tienen recursividad ni directa ni indirecta.

Factorización por la izquierda

Si mas de una regla de producción de la gramática tiene un prefijo común, entonces el parser top-down,  no puede tomar la decisión de cual producción debe tomar para parsear la cadena en cuestión.

Ejemplo

Si un parser top-down  encuentra una producción como esta:

A -> ab | ay | …

Entonces no puede determinar cual produccion seguir siendo que ambas producciones comienzan por el mismo terminal (o no-terminal). Para remover esta confusión utilizamos la técnica llamada “factorización”.

La factorización por la izquierda transforma una gramática para hacerla utilizable por un parser ‘top-down’. En esta técnica, hacemos una producción para cada uno de los prefijos comunes y para el resto de las derivaciones agregamos nuevas producciones.

Ejemplo

Las producciones anteriores podrían ser re-escritas así:

A -> aA'
A'-> b | y | … 

Y ahora el parser solo tendrá una producción por prefijo lo cual hace que sea más fácil tomar decisiones.

Conjuntos de primero y siguiente

Una parte importante de la construcción de una tabla de parser es crear los conjuntos de primero y siguiente. Estos conjuntos pueden determinar la posición actual de cualquier terminal en la derivación. Esto se hace para crear una tabla de parser que decida si se va a reemplazar T[A, t] = a con alguna otra regla de producción.

Conjunto primero:

Este conjunto es creado para saber cual es el símbolo terminal que se deriva de la primera posición para un no-terminal. Por ejemplo:

a ? t b

Eso es a deriva el terminal t en la primera posición, entonces t pertenece a FIRST(a).

Algoritmo para calcular el conjunto de primeros

La definición del conjunto de primeros es:

• Si ‘a’ es un no terminal, entonces PRIMERO(a) = {a}
• Si ‘a’ es un no-terminal y  a -> ? es una producción, entonces PRIMERO(a) = { ? }.
• Si ‘a’ es un no-terminal y a -> y1 y2 y3 … yn y cualquier PRIMERO(y) contiene a ‘t’ entonces ‘t’ esta en PRIMERO(a)

Puede ser visto asi:

PRIMERO(a) = {t|a -> tb} U { E | a -> e}

Conjunto de siguientes

Del mismo modo podemos calcular qué símbolo terminal sigue inmediatamente a un no-terminal ‘a’ en las reglas de producción. No consideramos que no-terminal puede generar, si no que miramos cuál sería el siguiente terminal que sigue las producciones de un no-terminal.

Algoritmo para calcular un conjunto de siguientes:

• Si ‘a’ es un símbolo inicial, entonces SIGUIENTE() = $
• Si ‘a’ es un no-terminal que tiene una producción a -> AB, entonces PRIMERO(B) es un SIGUIENTE(A) excepto en E.
• Si ‘a’ es un no-terminal y tiene la producción a -> AB, donde halla un BE, entonces SIGUIENTE(A) esta en SIGUIENTE(a).

El conjunto de siguientes puede ser canonizado como: SIGUIENTE(?) = { t | S *?t*}

Limitaciones del análisis sintáctico.

Los analizadores sintácticos reciben sus entradas de los tokens que generan los analizadores léxicos.  Los analizadores léxicos son los responsables de la validez de los tokens utilizados para analizar la sintaxis. Entonces los analizadores sintácticos tienen los siguientes inconvenientes:

• No puede determinar si un token es válido
• No puede determinar si un token ha sido declarado antes de usarlo
• No puede determinar si un token ha sido inicializado antes de ser usado.
• No puede determinar si una operación realizada en un token es válida o no.

Estas tareas son delegadas al analizador semántico, el cual estudiaremos en su respectiva sección.