Continuando con el estudio de la construcción de compiladores es necesario definir que son autómatas finitos deterministas y no deterministas.
Podríamos definir un autómata como una maquina de estados y transiciones dentro de la cual se tienen estados de aceptación y transiciones de un estado a otro siguiendo las reglas establecidas para grafos dirigidos. Dichos estados de aceptación dentro del automata “reconocen” que es posible aceptar una cadena de entrada, porque cumple con una definición en el alfabeto.
El modelo matemático de un automata consta de cinco elementos que son:
- Q = un conjunto finito de estados
- ? = un conjunto finito de símbolos de entrada
- q0 = un estado inicial
- qf = un conjunto de estados finales
- ? = una función de transición
Estos cinco elementos interactúan entre si para lograr un objetivo en común de la siguiente manera:
La función de transición (?) mapea el conjunto de estados finito(Q) a un conjunto de símbolos de entrada finito (?), Q × ? ? Q
Construcción de un automata finito
Sea L(r) un lenguaje regular reconocido por algún automata finito.
- Estados : Los estados del automata son representados por círculo. Los nombres de los estados están escritos dentro de esos círculos.
- Estado inicial: Estado en el cual el automata inicia. El estado inicial tiene una flecha apuntando hacia el.
- Estados Intermedios: Todos los estados intermedios tienen al menos 2 flechas; una apuntando hacia el estado y otra apuntando hacia otro estado.
- Estado Final: Si una cadena es parseada exitosamente, se espera que el automata quede en este estado. Se representa con un circulo doble. Puede tener una cantidad impar de flechas apuntando hacia el y una cantidad par de flechas apuntando hacia otros estados. El número de flechas impares es siempre uno mas que el de flechas pares.
- Transición : La transición de un estado a otro ocurre cuando un símbolo deseado es encontrado en la cadena de entrada. Después de una transición, un automata se puede mover al siguiente estado, o quedarse en el mismo estado. El movimiento de un estado a otro es representado por una flecha dirigida, esta flecha apunta al estado de destino. si el automata se queda en el mismo estado se dibuja una flecha que apuntara hacia el mismo.
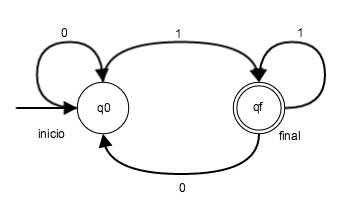
Ejemplo : Asumimos un automata finito que acepta un valor tres dígitos binarios que termina en 1. FA = {Q(q0, qf), ?(0,1), q0, qf, ?}
Podríamos mapear este automata a la siguiente expresión regular: (0|1)*1
Automata Finito Determinista (AFD) vs Automata Finito No Determinista (AFND)
AFD |
AFND |
|---|---|
| La transición desde un estado puede tener como destino un único estado. Por eso se llama determinista. | La transición desde un estado puede tener multiples destinos. Por eso se le llama no determinista. |
| No se aceptan transiciones con cadenas vacías. | Permite transiciones con cadenas vacías. |
| Se permite el uso de backtracking | No siempre se permite el uso de backtracking. |
| Requiere mas espacio. | Requiere menos espacio. |
| Una cadena es aceptada si su transición es hacia un estado final. | Una cadena es aceptada si solo una de todas sus posibles transiciones son hacia un estado final. |
Criterios de aceptación para un AFD y un AFND
Una cadena es aceptada por un AFD/AFND si el AFD/AFND que comienza en un estado inicial finaliza en un estado de aceptación (cualquiera de los estados finales) después de leer la cadena completa.
Entonces en términos matemáticos:
una cadena S es aceptada por un AFD/AFND (Q, ?, ?, q0, F), si:
?*(q0, S) ? F
El lenguaje L aceptado por un AFD/AFND es:
{S | S ? ?* and ?*(q0, S) ? F}
Una cadena S no es aceptada por un AFD/AFND (Q, ?, ?, q0, F), si:
?*(q0, S?) ? F
El lenguaje L? no es aceptado por un AFD/AFND (complemento del lenguaje L) es:
{S | S ? ?* and ?*(q0, S) ? F}
interezante
Con un olor a culo de recuerdos informaticos