El tiempo siempre debe estar en la mente de un programador. Es decir, ahorrar más a los usuarios y clientes. Cuanto menos tiempo pasen los usuarios esperando, más tiempo dedicarán a hacer cosas útiles con su producto o servicio.
Al igual que con todos los aspectos de la vida, hay muchas formas de resolver un desafío de programación. Y, al igual que en la vida real, el método que elija podría afectar directamente el tiempo que lleva resolver su problema. En este artículo, exploraremos el concepto de eficiencia dentro de la informática y aprenderemos algunas formas de medir y describir esta eficiencia. Al comprender cuán eficientes son nuestros algoritmos, podemos tener una idea de dónde podemos querer refactorizar nuestros procesos para obtener tiempos de ejecución más rápidos.
Conceptos
Bien, entonces necesitamos una forma de comparar fácilmente dos algoritmos en términos de su eficiencia. Podríamos intentar comparar los tiempos de ejecución reales de nuestras funciones, pero este método tiene problemas. No podemos responder de forma directa y coherente a la pregunta “¿cuánto tiempo tarda en ejecutarse mi código?” porque depende de demasiadas variables. La velocidad de su computadora, si está ejecutando otras aplicaciones al mismo tiempo, qué lenguaje de programación está utilizando, son factores que determinan el tiempo de ejecución real de su código. Entonces, en lugar de hacer esta pregunta directamente, hacemos una pregunta similar: “¿Cómo crece el tiempo de ejecución de mi función a medida que aumenta el tamaño de mi entrada?”. Esto resulta ser una pregunta mucho más importante de responder cuando se piensa en cómo funcionará nuestro algoritmo a escala, en lugar de comparar un tiempo de ejecución único de un algoritmo con un tiempo de ejecución único de otro, lo que realmente no nos da toda la información que necesitamos. Por ejemplo, podríamos tener un algoritmo que tenga un tiempo de ejecución muy rápido para entradas pequeñas, pero ese tiempo podría aumentar exponencialmente a medida que aumenta el tamaño de nuestra entrada.
Complejidad en el tiempo
El término que usamos para describir cómo funciona nuestro algoritmo en diferentes tamaños de entrada es su complejidad de tiempo. La complejidad del tiempo es una forma de etiquetar, en un lenguaje sencillo, cómo aumenta el tiempo de ejecución de una función a medida que aumenta el tamaño de nuestra entrada. Algunos ejemplos de etiquetas de complejidad de tiempo son tiempo constante, tiempo logarítmico, tiempo lineal y tiempo cuadrático (solo por nombrar algunos). Estas etiquetas describen la relación entre el tamaño de nuestra entrada y nuestro tiempo de ejecución, y es posible que observe que también describen la forma de varios tipos de líneas en una gráfica bidimensional. Esto nos brinda una manera excelente y fácil de visualizar cómo cambia nuestro tiempo de ejecución con respecto al tamaño de entrada. Más sobre esto en un momento.
Notación O Grande
La notación O Grande es una forma de describir matemáticamente esta relación, y se ve así: O (1), O (log n), O (n), O (n²), etc., todos representan una relación de complejidad temporal diferente ( tiempo constante, tiempo logarítmico, etc.).
Podemos usar la notación O Grande para describir la complejidad del tiempo en los escenarios mejor, promedio y peor de los casos, pero casi siempre solo nos preocupa el peor de los casos. Como hemos dicho, un algoritmo puede tener tiempos de ejecución muy rápidos para entradas pequeñas (en el mejor de los casos), pero tiempos de ejecución drásticamente peores para las más grandes (el peor de los casos), por lo que siempre es importante saber cómo funcionará su código en las circunstancias más difíciles. .
Es muy común que se le pida que analice la complejidad de su algoritmo en entrevistas técnicas. Por lo general, esperan una respuesta en notación Big O.
Como Interpretarlo
La sintaxis de O Grande es bastante simple: una O grande, seguida de paréntesis que contiene una variable que describe nuestra complejidad de tiempo, normalmente anotada con respecto a n (donde n es el tamaño de la entrada dada). Cualquier operador en n, n², log (n) – describe una relación en la que el tiempo de ejecución se correlaciona de alguna manera no lineal con el tamaño de entrada.
Aquí hay una descripción general rápida de las complejidades de tiempo más comunes / notaciones Big O y lo que significan en términos de tiempo de ejecución:
O(1)
Tiempo constante: la mejor complejidad posible, el tiempo de ejecución no se ve afectado por el tamaño de entrada. Esto implica que el número de operaciones que realiza el algoritmo no depende del tamaño de la entrada. Por ejemplo, si nuestra función tarda una cantidad de tiempo X en ejecutarse para 10 elementos y la misma cantidad de tiempo X en ejecutarse para 100 elementos y 1000, entonces parece que nuestro algoritmo se ejecuta en tiempo constante.
O(log n)
Tiempo logarítmico: esencialmente, el tiempo de ejecución crece en proporción al logaritmo del tamaño de entrada. Por ejemplo, si nuestra función tarda X cantidad de tiempo en ejecutarse en 10 elementos, y luego para 100 elementos toma 2X, y para 10,000 toma 4X, parece que nuestro algoritmo se ejecuta en tiempo logarítmico.
O(n)
Tiempo lineal: el tiempo de ejecución aumenta linealmente con el tamaño de la entrada. Por ejemplo, si nuestra función se ejecuta en X tiempo para 10 muestras, 5X para 50 muestras y 10X para 100.
O(n²)
Tiempo cuadrático: el tiempo de ejecución es proporcional al cuadrado del tamaño de entrada. El ejemplo más común de tiempo de ejecución cuadrático en el código es el infame doble bucle for.
Como regla general, los algoritmos que se ejecutan en tiempo cuadrático o peor son “lentos” y deben refactorizarse si es posible.
Encontrando la complejidad
Para comprender cómo estas diferentes complejidades temporales se manifiestan en la naturaleza, escribamos algunas funciones y recorramos dos enfoques para analizar su complejidad.
Enfoque fácil: visualizar
Una forma ingenua, aunque efectiva, de verificar la complejidad de su algoritmo es simplemente trazar el tiempo de ejecución de su función en diferentes longitudes de entrada.
Digamos que queremos escribir una función que nos dé la suma de cualquier arreglo unidimensional dado (por supuesto, podríamos usar la funciones incorporadas como sum() de Python, pero vamos a darle un enfoque ingenuo). Llamaremos a esa función get_sum().
const get_sum = (array) => {
total = 0
for(x in array) {
total = total + array[x]
}
return total
}
Ahora, queremos saber qué tan eficiente es nuestro algoritmo. Registramos el tiempo de ejecución de nuestra función para un rango de longitudes de entrada y graficamos los resultados.
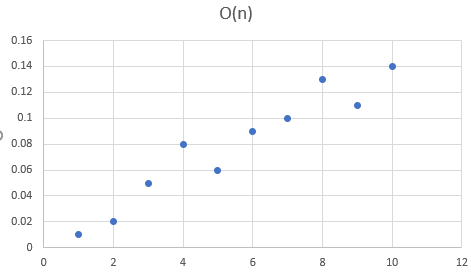
Genial!, aparte de algunos valores atípicos, ¡parece una línea recta! Esto implica que nuestro tiempo de ejecución es lineal (el tiempo de ejecución reacciona linealmente a la longitud de la entrada). La intuición aquí es que tenemos un bucle for, que procesa cada elemento en nuestra matriz de longitud n. Por lo tanto, nuestra complejidad de tiempo con respecto a n sería simplemente lineal, o O(n)
Probemos con otro. En lugar de calcular la suma de nuestra entrada, escribamos una función sin sentido que solo tome nuestra matriz la asigne a una variable y regrese esa variable. Llamaremos a esta función no_op().
const no_op = (array) => {
const nuevo_array = array
return nuevo_array
}bueno es una función que no tiene sentido pero es para efectos académicos únicamente. veamos como se comporta cuando la llamamos n veces
A diferencia de nuestra función get_sum(), nuestra función no_op() no tiene bucles for. De hecho, ni siquiera realizamos ninguna operación importante. Visualicemos el tiempo de ejecución de este algoritmo para una variedad de longitudes de muestra.
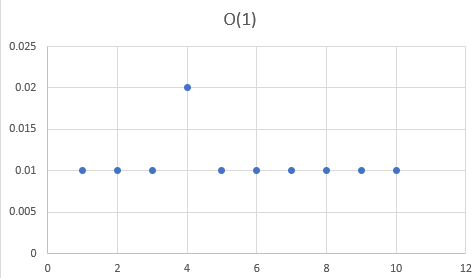
Nuestro gráfico de tiempo de ejecución es prácticamente una línea horizontal, lo que implica que nuestro tiempo de ejecución no se ve afectado por la longitud de nuestra entrada. Así es como se vería si un algoritmo se ejecutara en tiempo constante.
Calcular la complejidad
En lugar de crear un proceso completamente separado para visualizar nuestros tiempos de ejecución e inferir nuestra complejidad, existe un método muy simple para calcular la complejidad de cualquier algoritmo. Al igual que en nuestros gráficos anteriores, podemos describir la complejidad de nuestro algoritmo en función de sus operaciones en la entrada. Después de que tengamos esta función que describe nuestro tiempo de ejecución como una función del tamaño de entrada, podemos seguir dos pasos simples:
- Encuentre el término de más rápido crecimiento
- Eliminar cualquier coeficiente
Esto puede no tener absolutamente ningún sentido en este momento, pero tengan paciencia conmigo, lo tendrá. Volvamos a nuestra función get_sum(). Recuerde que se veía algo como esto:
const get_sum = (array) => {
total = 0
for(x in array) {
total = total + array[x]
}
return total
}
Ahora, vayamos línea por línea y tomemos nota de las operaciones que se realizan en nuestra entrada. Podemos ver cuántas veces nuestras operaciones procesan una entrada y asignar rápidamente una notación Big O a cada operación con respecto a cómo se utiliza la entrada. Luego, usaremos estas complejidades individuales para calcular el Big O para todo nuestro algoritmo.
//no depende de la matriz, el tiempo de ejecución siempre será el mismo o "constante"
total = 0
// -> O(1)
//haga lo siguiente n número de veces (donde n es la longitud de la matriz)
for(x in array) {
// -> O(n)
//sumarvalores (a menos que sean drásticamente más grandes o más pequeños entre sí) toma aproximadamente la misma cantidad de tiempo
total = total + array[x]
// -> O(1)
}
// devolviendo un valor toma un tiempo constante
return total
// -> O(1)Recuerde que podemos pensar en estas operaciones como variables en una función para determinar nuestro tiempo de ejecución. Usando este método, podemos representar el tiempo de ejecución T de nuestra función get_sum() de la siguiente manera:
T = O(1) + O(n) + O(1) + O(1)
Debido a que O(1) representa una relación invariable o independiente con n, nuestro tamaño de muestra, podemos tratarlo como una constante. Nuestra función para T se puede reescribir como:
T = n + c1 + c2 + c3
Ahora que tenemos nuestra función que representa el tiempo de ejecución T como una función de la longitud de entrada n, seguimos nuestros dos pasos.
Primero, encuentre el término de más rápido crecimiento. Para la función anterior, debido a que c, c2 y c3 son todas constantes, no crecen. Por lo tanto, podemos ver que el término de más rápido crecimiento es n. Bien hecho.
Paso dos, elimine los coeficientes. Nuestro coeficiente es cx, que representa una complejidad de O (1), por lo que eliminamos eso. Lo que nos queda lo ponemos entre paréntesis de nuestra notación Big O, dejándonos con nuestra respuesta de O (n), o tiempo lineal. ¡Parece que nuestros dos métodos están de acuerdo!
Podemos seguir estos mismos pasos sencillos para encontrar la complejidad de prácticamente cualquier algoritmo.

