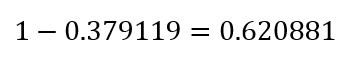La paradoja del cumpleaños

Hace unos días felicitaba a un colega por su cumpleaños, y entre la platica absurda de informáticos salio el típico tema “ojala fuéramos millonarios”, y pues el me comentaba que justo el día de su cumpleaños había comprado un numero de la lotería, pero que luego se acordó que era su cumpleaños y bueno se puso a calcular la absurda probabilidad de que después de haber comprado números de la lotería toda su vida se la ganase justo el día de su cumpleaños.

No se si el quería traer el tema de la paradoja del cumpleaños a la conversación,  pero no pude evitar recordarla y discutirla en este mi espacio blogero.

Que es la paradoja del cumpleaños?

Bien la paradoja del cumpleaños resulta de comparar las probabilidades de que dos individuos compartan la misma fecha de cumpleaños bajo dos universos distintos, siendo un universo el de toda la población mundial y un universo reducido a 20 personas (por ejemplo, aunque podrían ser mas personas).

Supongamos que vas por la calle y le preguntas a un individuo aleatorio cuando es su cumpleaños: Bien la probabilidad de que ambos cumplan años en la misma fecha es de 1/365, es decir aproximadamente 0.27%

No obstante si juntas a 20 personas en una oficina y pones un gran calendario, y le preguntas a una persona que marque su fecha de cumpleaños con una X, entonces la siguiente persona que marque su cumpleaños solo tendra 364 dias disponibles, asi que la probabilidad de que las fechas no coincidan es de 364/365, aun asi es bastante baja, pero como tenemos 20 personas la probabilidad de que coincidan se define de la siguiente forma:

Si evaluamos la multiplicación para 20 personas nos da un total:

Es decir aproximadamente un 62% de que entre 20 personas al menos 2 compartan la misma fecha de cumpleaños.

bastante interesante… un problema sencillo aparentemente sin aplicación alguna en la vida real (al menos para los pobres mortales), por diversión he aquí una función en python que calcula la paradoja del cumpleaños paso por paso:

def paradoja(n):
    p = 1.0
    i=0
    for i in xrange(1, n):
        p = p * (366 - i) / 365
        print '%3d : %10.6f' % (i, 1-p)

paradoja(20)

Todo muy lindo, pero para que sirve?

Bien en criptografía tenemos la denominada encriptación simétrica, que es la técnica de codificar mensajes utilizando una llave común, esta “llave” en realidad es un complejisima función matemática que no vamos a explicar aquí porque a parte de que no solo existe un tipo de función,  es un tema ajeno a la paradoja del cumpleaños que estoy tratando de explicar. Entonces la paradoja del cumpleaños nos sirve para realizar los denominados “ataques de cumpleaños”o en ingles “birthday attack” que se valen de la matemática de esta paradoja para romper funciones criptográficas.

Como así? supongamos que tenemos una función  F  hipotética que genera un hash de 64 bits, eso significa que la función tendra un total de 1.8 × 10¹⁹ resultados posibles, y el ataque consiste en hallar un x₁ y un x₂ tales que f(x₁) = f(x₂), Si todos los hash son igualmente probables (el mejor de los casos), entonces tomaría solamente unos 5.1 × 10⁹ intentos aproximadamente generar una colisión usando fuerza bruta.

Veamos un ejemplo de la vida real! con la mundialmente famosa función md5 la cual cientos de miles de sitios usan para encriptar contraseñas.

Supongamos que tenemos las siguientes clave diferentes:

• 4dc968ff0ee35c209572d4777b721587d36fa7b21bdc56b74a3dc0783e7b9518afbfa200a8284bf36e8e4b55b35f427593d849676da0d1555d8360fb5f07fea2
• 4dc968ff0ee35c209572d4777b721587d36fa7b21bdc56b74a3dc0783e7b9518afbfa202a8284bf36e8e4b55b35f427593d849676da0d1d55d8360fb5f07fea2

ambas generan el mismo hash:

• cee9a457e790cf20d4bdaa6d69f01e41

Si quieren indagar mas sobre el asunto, vean este link de donde saque este ejemplo y esta con todo y su código fuente https://marc-stevens.nl/research/md5-1block-collision/ es el código que usaron para encontrar esta colisión.

Seria interesante ver mas ejemplos, si ustedes saben de alguno compartanlo en los comentarios :3